Stereoloji, üç boyutlu örneklerin (biyolojik yapılar, metalurjik örnekler vb.) iki boyutlu kesitlerinden elde edilen verilere dayanarak, onların gerçekteki üç boyutlu özellikleri ile ilgili yorumlar yapılmasını sağlayan bilim dalının adıdır. (konuyla ilgili video dersleri için tıklayınız. Ayrıca bkz: Stereoloji Sözlüğü)
Kesitler, herhangi bir yapının içinden geçen ve yapının bileşenleri ile kesişen düzlemler olarak düşünülürse, yapının her bir bileşeni, bu kesitlerde, sayısı, büyüklüğü ve kapladığı uzunluk, alan ve hacim oranıyla ilişkili bir biçimde izdüşümler (profiller) oluşturur. Bu izdüşümler de yapının içerdiği bileşenler hakkında bilgi almak üzere kullanılır. Fakat, yapının içinde bulunan bileşenlerin kesitlerde ortaya çıkan izdüşümleri, sadece ait oldukları yapıların, kesit düzlemi üzerindeki temsillerinden ibarettirler. Dolayısıyla, bu izdüşümlerden yola çıkarak doğrudan yorumlar yapmak, bunların ait oldukları bileşenlerin üç boyutlu özelliklerine ait gerçek verilerin elde olmamasından dolayı, oldukça yanıltıcı olabilmektedir (Şekil-1).
 |
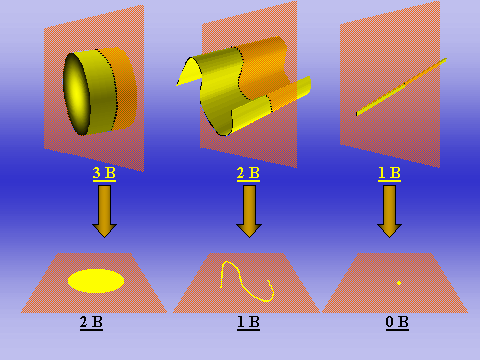| Şekil-1: İki boyutlu kesitlerle yapılan örneklemelerde ortaya çıkan boyut azalması. Herhangi bir yapı, iki boyutlu bir düzlemle kesişmesi durumunda, normalde üç boyutlu uzaydaki n boyutlu yapısına bağlı olarak, “n-1” boyutlu bir kesişim (izdüşüm) verir. Dolayısıyla iki boyutlu kesitlerde, hacme sahip 3 boyutlu yapılar iki boyutlu alanlar; iki boyuta (en ve boy) sahip alanlar tek boyutlu çizgiler; ve tek boyutlu çizgiler ise boyutsuz (sıfır boyutlu) noktalar olarak örneklenirler. Bu durum biyolojik dokulara uyarlanacak olursa: Bir hücre (3 boyutlu), kesitte bir alan; bir zar bir çizgi (çekirdek zarı gibi) ve (tam olmasa da ideal anlamında bir çizgi olan) bir fibril de bir nokta olarak ortaya çıkacaktır. Bu prensibe göre boyutsuz (sıfır boyutlu) varlıklar, iki boyutlu kesitlerle örneklenemezler. Sayı kavramı da, boyutsal özelliklerden bağımsız (yani sıfır boyutlu) olduğundan, iki boyutlu kesitlerden faydalanılarak, doğrudan sayı kavramına ulaşmak imkansızdır. Sayı ancak üç boyutlu bir örnekleme sondası ile örneklenebilir. |
 |
| Şekil 2. Taneciklerin yöneliminin kesitlerle örneklenme şansına etkisi. Birbirine paralel ve eşit aralıklı kesitlere ayrılmış olan bir referans hacim içerisindeki iki partikülden büyük olanı, küçük olana göre daha fazla kesit tarafından örneklenme şansına sahiptir. Dolayısıyla, büyük partikül daha fazla kesitte izdüşümleri ile temsil edileceğinden, kesitlerde ortaya çıkan partikül izdüşümlerinin sayısının gerçek partikül sayısıyla doğrudan bir ilişkisinin olmadığı açıktır. |
 |
| Şekil 3. Tanecik büyüklüğünün örneklenme şansına etkisi. Kesit alma doğrultusuna göre partiküllerin yönelimlerinin, örneklenme ihtimali ile olan ilişkisi şematize edilmiştir. Uzun ekseni kesit alma doğrultusuna paralel olan, veya, kesit düzlemine dik olarak yerleşim gösteren partiküller, eğik veya kesit düzlemine paralel yerleşmiş olanlara göre daha fazla kesit tarafından isabet alma şansına sahip olacaklardır. Sonuçta, partiküllerin kesitlerde ortaya çıkan izdüşümlerinin sayısı (yani partiküllerin seri kesitler tarafından örneklenme ihtimali), partiküllerin boyutları ve yönelimlerinin de etkili olduğu bir parametredir ve bu parametreden yola çıkılarak partikül sayısına ulaşmak istendiğinde, izdüşüm sayısına etkide bulunan bu faktörleri ortadan kaldırabilecek bir örnekleme mantığı uygulanmalıdır. Bu da ancak, iki boyutlu kesitler bu tip yanıltıcı bilgiler içerdiğinden, üç boyutlu örnekleme stratejileri ile gerçekleştirilebilir. |
Bu basit örnek dışında, iki boyutlu düzlemler üzerindeki izdüşümlerden, bu izdüşümlerin ait oldukları yapılar hakkında bir fikir yürütmenin söz konusu olduğu hemen hemen tüm durumlarda, bu veya benzeri sorunlar araştırıcıların karşısına çıkmaktadır. Sözgelimi, boyut azalması prensibi bunlardan bir tanesidir ve belki de kesitlerle çalışmanın getirdiği problemleri teorik planda anlamak için en önemlilerinden birisidir. İki boyutlu kesit düzlemleri ile örneklenen “n” boyutlu bir yapı, kesitte “n-1” kadar boyuta sahip bir izdüşüm ile temsil edilecektir. Yani, belli bir hacme sahip (üç boyutlu) katı bir öğe, iki boyutlu bir yüzey; iki boyuta sahip bir yüzey (örneğin bir membran) tek boyutlu bir çizgi veya eğri; tek boyutlu (fibril gibi) bir çizgi veya eğri ise, sıfır boyutlu bir nokta olarak izdüşüm verir (Şekil-1). Tek başına bu bakış açısı bile, kesitlerden faydalanılarak yapılan morfometrik çalışmaların, uygun metotlar kullanılmadan ne kadar yanıltıcı olabileceğini göstermeye yeterlidir.
Stereoloji ise etkin (daha kısa zamanda daha az hatalı iş yapmayı sağlayan) ve tarafsız (gerçek değerden sistematik bir sapmaya sebep olmayan) metotları ile, bu ve benzeri problemleri ortadan kaldırmak üzere geliştirilmiş kurallar bütününü içeren bir bilim dalıdır.
Gerçekte "kesit" kavramı, herhangi bir katı yapı içerisinden geçen ve kalınlığı olmayan (t=0 olan) düzlemleri ifade eder. Buna iyi bir örnek olarak, bir maden örneğinin kesilmiş ve parlatılmış bir yüzeyi verilebilir. Maden örnekleri ışığa geçirgen olmadıklarından bu örnekleri inceleyen bir gözlemci, parlatılmış yüzeye karşılık gelen gerçek iki boyutlu bir düzlemle karşı karşıyadır. Halbuki biyolojik örneklerden alınan kesitler, aslında belli bir kalınlığa sahip olan dilimlerdir. Kalınlıkları ne kadar küçük olursa olsun, doğrudan iki boyutlu düzlemler olarak değerlendirilemezler. Dolayısıyla biyolojik örneklerden alınan kesitler, ister ışık, ister elektron mikroskobu için olsun, kalınlıkları da dikkate alınarak değerlendirilmelidirler (Howard ve Reed, 1998).
Genel bir kabul olarak, eğer incelenilen bir yapı, çıplak gözle, ilgilenilen tüm ayrıntıları seçilebilecek büyüklükte ise, herhangi bir yanılmaya meydan vermeyecektir. Fakat, mikroskobik düzeyde yapılan incelemeler söz konusu olduğunda, bir çok yanıltıcı faktör devreye girmektedir. Eğer bunların farkına varılarak mantıklı önlemler alınmaz veya düzeltmeler yapılmazsa, elde edilmek istenen sonuç, gerçek değerden istenmeyen sapmalar gösterebilir.
Hata kaynakları çeşitli olmakla beraber, en fazla karşılaşılanı, çalışılan yapı ile ilgili çeşitli ön kabullerin yapılması ve kesitlerden elde edilen verilerin gerçek üç boyutlu yapı ile ilgili özelliklerle ilişkilerinin tam olarak anlaşılamamasıdır. Eğer bu ve buna benzer hata kaynakları görmezden gelinir veya gözden kaçırılırsa, sistematik bir biçimde gerçek değerden sapmalar olabilecektir. Böyle bir yaklaşımda, kesin olarak yanlış sonuçlar elde edilebileceğini söylemek mümkün değilse de, tesadüfi olarak gerçek sonuçların elde edilmesi durumunda dahi, hataların etkileri gizli ve belirlenemez olduğu için, sonuçların ne derece gerçeği yansıttığı belirlenemeyeceğinden, bu tip bir çalışmanın güvenilirliğinden de söz edilemez. Bu durum hız göstergesi bozuk bir arabayla yol almaya benzetilebilir (Howard ve Reed, 1998). Sözgelimi, arabanın hız göstergesi, +20 km/saat'lik bir sabit yanılmaya sahip olsun. Sürücü, hız göstergesinden 80 km/saat'lik bir hız okuduğunda, arabanın aslında 100 km/saat'lik bir hızla seyrettiğini anlayamayacaktır. Çünkü buradaki yanılmayı saptamak için herhangi bir başka başvuru kaynağı mevcut değildir ve hızdaki hata, sürücünün gözünden tamamen gizlidir. Ancak dışarıdan hız ölçümü yapan bir polis aracının doğru kalibre edilmiş radarına yakalanıp ceza ödemek durumunda kaldığında, bu hatanın farkına varabilir.
Stereolojide, böyle hata kaynaklarından etkilenmesi muhtemel olan yöntemler taraflı (biased) metodlar olarak nitelendirilmektedir. Dolayısıyla taraflı terimi "gerçek değerden sistematik sapma gösteren" manasındadır. Stereolojik metotlar ise, tarafsız (unbiased) metotlardır. Bunun anlamı; stereolojik metotlar kurallarına uygun bir biçimde uygulandığında, sistematik hatadan bağımsız sonuçlar elde edilmesini sağlar ve örnekleme sayısı arttırıldıkça gerçek değere daha fazla ihtimallikle yaklaşmak mümkün olur.
 |
| Şekil 4. Sistematik rastgele örnekleme yaklaşımının çalışmadaki her basamakta uygulanması. |
Stereolojik metotların temelini “Sistematik Rasgele Örnekleme” (SRÖ) stratejisi oluşturmaktadır. Bu örnekleme biçiminin temel özelliği , çalışılacak olan yapıdan örnekler almanın gerekli olduğu durumlarda, yapının her noktasının eşit örneklenme şansına sahip olmasını sağlamasıdır. Biyolojik yapılar, genellikle, içerdikleri ve araştırıcı için inceleme konusu olan bileşenlerine göre (hücre, çekirdek, vezikül vb.) çok büyük olduklarından, yapıdan elde edilen tüm kesitlerin çalışmaya dahil edilerek değerlendirilmesi, pratik olarak imkansızdır. Sözgelimi, insan neokorteksindeki toplam nöron sayısını tesbit etmeye yönelik bir çalışma için, çalışılacak beyinlerden alınacak onbinlerce histolojik kesit tek tek incelenemez. Bu durumda elde edilebilecek muhtemel örnekler (kesitler) arasından belli oranlarda bir seçim yapılması gerekecektir. Bu seçim yapılırken, seçilen örneklerin, söz konusu yapıyı en iyi biçimde temsil edebilmesi için, yapının her bir noktasının eşit örneklenme şansına sahip olması, istatistiksel bir zorunluluktur. Bu şartı sağlamak üzere, rasgele seçimler yapmak da, tam olarak sorunu çözememektedir. İşte SRÖ'nin önemi burada ortaya çıkar. SRÖ, önceden belirlenmiş sabit bir örnekleme aralığı boyunca, ilk aralık içinden rasgele bir noktadan başlanmak suretiyle, ilgilenilen yapının tamamının örneklenmesini içerir. Önceden belirlenen örnekleme aralığı (örneğin, her onuncu kesiti veya parçayı seçmeye karar verildiğinde ilk on kesitlik seri), örneklemenin sistematik kısmını, ilk aralık içinde rasgele bir noktadan başlanması (örneğin, ilk on kesit içinden herhangi birinin başlangıç olarak seçilerek, bu kesitten sonra gelen her onuncu kesitin örnek olarak seçilmesi) ise, örneklemenin rasgelelik özelliğini sağlar. İstatistiksel bakış açısıyla, bu tip bir örnekleme, ne kadar çok örnek üzerinde uygulanırsa, yapının her noktasına eşit örnekleme şansı tanıdığı için, homojen ve verimli bir örnekleme elde etme şansı da o kadar artar (Gundersen ve Jensen 1987).
Stereolojik metotlarda kullanılan yöntem ve prensiplerin büyük bir kısmı, SRÖ mantığının çeşitlemeleri olarak düşünülebilir. Tanecik sayımı, alan hesaplamaları, alan ve hacim oranları gibi hesaplamalarda, ilk şart, çalışılan yapının her aşamada (parçaların seçimi, kesitlerin örneklenmesi, sayım alanlarının ve alan örneklerinin belirlenmesi vb.) sistematik ve rasgele bir tarzda örneklenmesidir (Stereolojik metotlarla ilgili genel değerlendirme (review) çalışmaları için bkz. Sterio, 1984; Gundersen, 1977, 1986, 1992; Gundersen ve ark., 1988a, 1988b; Royet, 1991; Mayhew, 1991, 1992; West, 1993, 1994; Oorschot, 1994; Cruz-Orive ve Weibel, 1990; Cruz-Orive, 1995; Mayhew ve Gundersen, 1996; Mayhew, 1996).
Tanecik (partikül) Sayısı:
Biyolojik yapılardaki taneciklerin toplam sayılarının veya birim hacme düşen sayısal yoğunluklarının (NV) belirlenmesi, bir çok çalışma için vazgeçilmez bir parametredir. Özellikle sinir sisteminde, temel işlevsel elemanlar olan sinir hücrelerinin sayıları, araştırmalarda sıklıkla, önemli bir veri olarak gündeme gelmektedir. Yapı ve fonksiyon arasındaki ilişkilerin önemli bir ifadesi olarak yorumlana gelen sayı kavramı, organların gelişimi, dönemsel fonksiyon değişiklikleri, kimyasal maddelerin ve fiziksel muamelelerin etkileri, uyumsal özelleşme (adaptive specialization), öğrenme ve hafızalama, hastalık oluşum mekanizmaları ve yaşlanma gibi bir çok araştırma konusu için, üzerinde yorumlar yapılan araştırma verilerinden birisidir. Sayı kavramı bu denli önemli olmasına rağmen, uzun yıllar boyunca, tanecik sayımlarını, kabul edilebilir bir hata payı sınırı içerisinde tutmayı sağlayacak bir yöntem ortaya konamamıştır.
Tanecik sayımı yapmak için, ilgilenilen yapılardan kesitlerin alınması gerekir. Fakat bu kesitler, sadece görüntü olarak değerlendirildiklerinde, üç boyutlu bir ortamda dağılmış olarak bulunan sıfır boyutlu sayı kavramını örnekleyemeyen, iki boyutlu görüntülerdir. Taneciklerin kesitlerde ortaya çıkan izdüşümlerinin doğrudan sayılmasıyla tanecik sayısına ulaşma girişimi, ilk denenen yöntemlerden biridir. Fakat sayım işiyle uğraşan araştırıcıların, izdüşüm sayısı ile tanecik sayısının doğrudan ilişkili olmadığını fark etmeleri uzun zaman almamıştır. Tanecik sayısı, taneciğin büyüklüğü veya yönelimi gibi üç boyutlu etkilerden bağımsız olarak örneklenmesi gereken sıfır boyutlu bir niceliktir. Sıfır boyutludur, çünkü, herhangi bir taneciğin boyutsal özellikleri (büyüklük, uzunluk, çap, hacim vb.) ne olursa olsun, sayı söz konusu olduğunda değeri 1(bir)dir. Yani sayı, boyutsal özelliklerden bağımsızdır. Fakat yapılardan elde edilen kesitler, iki boyutlu düzlemler olarak kabul edilir ve tanecikleri boyutsal özellikleriyle yakın ilişkili bir biçimde örneklerler. Bir yapıdan geçen seri ve eşit aralıklı kesitler, büyük tanecikleri küçük olanlara, kesit alma doğrultusuna dik doğrultuda yerleşmiş olanları paralel doğrultuda yerleşmiş olanlara göre daha fazla miktarda örnekler. Yani bir taneciğin bir kesit tarafından isabet alma şansı, o taneciğin çapına, yüksekliğine (hacmine) ve yönelimine (orientation) bağlıdır (Mayhew, 1996) (Şekil-1, 2 ve 3).
 |
| Şekil 5. Sinir dokuya ait bir histolojik kesit. Sinir hücrelerinin gövdeleri (koyu kahverengi) çekirdeklerine göre (açık renk) daha fazla sayıda gözükme şansına sahiptir. |
Kesitler her ne kadar iki boyutlu düzlemler olarak kabul edilse de, sonlu kalınlığa sahip dilimler olduklarından, kalınlıkları da dikkate alınmalıdır. Eğer kalınlık ihmal edilerek kesit görüntüleri iki boyutlu düzlemler olarak değerlendirilirse, kalınlığın tanecik sayısına olan etkisi, sayımda hatalara sebep olabilir. Kesit kalınlığı arttıkça, taneciklerin kesitler içerisinde görülme sıklığı artacaktır. Histolojik kesitler, şeffaf olduklarından, bu artış, izdüşüm sayısının artışı olarak ortaya çıkar (Şekil-12). Kesit kalınlığına bağlı olarak oluşan bu duruma fazla görünme (over-projection; eski adıyla Holmes Etkisi) adı verilir. Holmes etkisinin fark edilmesinin ardından, araştırıcılar bir çok düzeltme faktörleri kullanarak, bu problemin üstesinden gelmeye çalışmışlardır. Bunlardan en ünlüsü ve belki de en çok kullanılanı, Abercrombie'nin düzeltme faktörüdür. Abercrombie, 1946 yılında yayınladığı ünlü çalışmasında, kesit kalınlığına ve tanecik büyüklüğüne bağlı olarak ortaya çıkan sayım hataları üzerinde durmaktadır. Buna göre, sayımı yapılan taneciklerin gerçek sayısı; sayım sonucunda elde edilmiş olan tanecik veya tanecik parçalarının sayısının, kesit kalınlığı / (kesit kalınlığı x tanecik yüksekliği) şeklinde ifade edilen bir düzeltme faktörü ile çarpımına eşit olmalıdır. Bu ifade, şu şekilde formüle edilmektedir.
Abercrombie’nin düzeltme faktörü, yayınlandığı tarihten günümüze kadar çok fazla sayıda çalışmada referans olarak gösterilmiştir. Stereolojik metotların uygulama alanı bulmasından sonraki yıllarda bile, yetersiz olan özellikleri ortaya konmuş olmasına rağmen, yine bir çok araştırıcı tarafından kaynak olarak gösterilmeye devam edilmiştir (Williams ve Rakic, 1988).
Gerçekte, Abercrombie ve diğer araştırıcıların önerdikleri düzeltme faktörleri, hatalı sonuçlar elde edilmesine sebep olabilmektedir. Abercrombie tarafından önerilen düzeltme faktörü, diğer araştırıcıların önerdikleri metotların esasını oluşturduğundan, bu metodun hataya yol açan özelliklerine göz atmak, hata kaynakları hakkında bir fikir edinmek için yeterli olacaktır.
Öncelikle, Abercrombie’nin yöntemi taraflıdır (gerçek değerden sistematik sapma göstermektedir). Bizzat Abercrombie, bu metodun, hücre sayısını %5-10 oranında fazla hesaplamaya meyilli olduğunu belirtmektedir (Abercrombie, 1946). Ayrıca, tanecik yüksekliği olarak adlandırılan değerin belirlenmesinde de önemli zorluklar mevcuttur. Bu değerin ölçülmesi, pratik olarak imkansız olduğu gibi, bazı durumlarda, tanecik yüksekliği yerine “tanecik çapı” ölçülerek kullanılmaktadır ki, özellikle taneciklerin küre şeklinde olmadığı, basık, köşeli yapıda veya büzülmüş olduğu durumlarda, bu iki değer arasındaki farklılık oldukça önemli hale gelmektedir (Williams ve Rakic, 1988). Aslında, kesit kalınlığı, yüksekliği en fazla olan taneciğin yüksekliğinden 1,5 kat veya daha fazla olduğu sürece, Abercrombie’nin düzeltme faktöründen kaynaklanan hesap hataları ihmal edilebilir boyutlarda kalır (Clarke, 1992). Fakat bu durum, hem her zaman gerçekleşmesi zor olan bir durumdur ve hem de, gerçek sayıya ulaşma için tüm teorik gereksinimleri yerine getirebilmek çoğu zaman mümkün olamamaktadır.
 |
| Şekil 6: Fazla görünme (overprojection veya eski adıyla Holmes) etkisi. Histolojik çalışmalar için alınan kesitler, gerçekte, belli bir kalınlığa sahip dilimlerdir. Bu kalınlık ise, özellikle partikül sayımlarında, bazı hatalara neden olabilecek bir yanılmanın da sebebidir. Kesit kalınlığı artıkça, kesitin kalınlığı içerisinde örneklenen partiküllerin sayısı artacaktır. Bu da, şeffaf olan histolojik örnekler, mikroskop altında, kalınlıkları dikkate alınmadan gözlendiklerinde, izdüşüm sayısının artması şeklinde kendini gösterecektir. Bu etki, partikül sayımlarında oldukça yaygın olarak hatalara sebep olur ve fazla görünme etkisi (overprojection) olarak bilinir (Royet, 1991’den değiştirilerek yeniden çizilmiştir). |
 |
| Şekil 7 : Sayısal yoğunluk verilerinden yola çıkılarak biyolojik yorumlar yapmanın yanlışlığı. Karşılaştırmalı çalışmalar yapmak, tıp ve biyoloji bilimlerinde en çok kullanılan yöntemlerden birisidir. Özellikle, herhangi bir maddenin, bir organ veya yapı üzerindeki etkileri, karşılaştırmalı çalışmalarla ortaya çıkarılmaya çalışılır. Bu çalışmalardan özellikle sinir sistemi alanında en fazla miktarda yararlanılırken, hücre sayısı veya hücrelerin birim hacimdeki sayıları (yani sayısal yoğunlukları) en fazla kullanılan parametrelerdir. Sayısal yoğunluk değeri, ancak, sayıları söz konusu olan partikülleri içeren yapının hacminde bir değişme olmadığı garanti edilebilirse, kullanılabilir. Aksi halde, sayısal yoğunluk değeri, tek başına, partikül sayısındaki değişme hakkında bir fikir veremez. A’da, herhangi bir maddenin etkisinin üzerinde denendiği bir yapı, maddenin verilmesinden önceki haliyle şematize edilmiş olsun. Aynı zamanda, kontrol grubundaki deneklerde de, yapı bu haliyle bulunmaktadır. Yapının içerisinde bulunan partiküller, birim hacimde belli bir yoğunluğa sahiptirler (çerçeve). B’de ise, maddenin uygulanmasından sonra, aynı yapı içerisinden eşit hacimde bir bölge örneklenmiştir (çerçeve). Fakat, verilen madde, hücre sayısını azaltmayıp, sadece yapının toplam hacmini (ödem vb gibi sebeplerle) artırdığı halde, aynı hacimde daha az sayıda partikül bulunmaktadır. Dolayısıyla, yapının toplam hacmindeki değişimden habersiz olan bir araştırıcı, bu maddenin, söz konusu bölgede partikül sayısının azalmasına sebep olduğu sonucuna rahatlıkla varabilir. Bu ise gerçeklerle bağdaşmadığı gibi, oldukça önemli hatalara da sebep olabilecek bir durumdur (Oorschoot, 1994’den değiştirilerek yeniden çizilmiştir). |
Abercrombie tarafından ortaya atılan düzeltme faktörü üzerinde bu kadar çok durulmasının sebebi, bu konuyla ilgili en iyi bilinen örnek olması ve diğer düzeltme faktörlerinin de benzer ön kabuller ve taraflı özellikler içermesidir. Tüm bu düzeltme faktörleri, farkına varılmış olan sayım hatalarının düzeltilmesi amacıyla ortaya atılan, fakat, özellikle yeni stereolojik metotların ortaya çıkışının ardından, eksik yönleri anlaşılmış olan metotlardır. Günümüzde artık bir standart olma yolunda ilerleyen stereolojik metotlar, tüm bu eksikliklerin üstesinden gelebilecek çözümler içermektedir.
Disektör (The disector)
Disektör ilk kez 1984 yılında Sterio tarafından tarif edilmiştir (Sterio, disektör sözcüğünün bir anagramı olup; stereolojik metotlara çok büyük katkıları bulunan ve halen bu konuda çalışmalarını sürdürmekte olan ünlü bir "Viking" stereolojistin takma adıdır). Bu yöntem, tanecik sayımında kullanılan sanal 3 boyutlu bir stereolojik sonda olarak da tarif edilebilir. Disektörün temel mantığı, taneciklerin kesit alma doğrultusu boyunca ilk ortaya çıktıkları veya son görüldükleri kısımları, yani taneciklerin “uçlarını” bulmaktır. Her taneciğin şekli ve yöneliminden bağımsız olarak, bir yönde bir tek ucu olduğu düşünülürse, bu mantıkla iş gören bir metot, gerçek tanecik sayısına ulaşılmasını sağlar.
Fiziksel Disektör (Physical disector)
Disektörün ilk ortaya çıkan biçimidir (Sterio, 1984). Bu yöntemde, iki tane ardışık veya birbirlerinden belli bir uzaklıkla ayrılmış olan iki kesit alınır, birinde bulunup, diğerinde bulunmayan tanecikler sayılır. İki kesit arasındaki mesafe “disektör yüksekliği” adını alır ve yapılan sayım sonucunda, disektör yükseklikleri boyunca örneklenebilen disektör taneciklerinin, yani, tanecik uçlarının sayısı bulunur. Bu da, çalışılan taneciklerin sayısal yoğunluğunu (NV) verir.
Disektörün temel uygulanma şekli, aralarında asgari tanecik yüksekliğinden daha az bir mesafe olan iki kesitin alınarak karşılaştırılmaları şeklindedir. Kesitler arası mesafenin, minimum tanecik çapından küçük olmasının gerekmesi, taneciklerin, kesitler arasında kesilmeden –yani örneklenmeden- atlanmaması amacına yöneliktir. Tek bir taneciğin bir kesit tarafından isabet alması, o taneciğin kesit alma doğrultusundaki yüksekliğine bağlıyken; “bir kesit tarafından kesilip ardışık paraleli tarafından kesilmeme” şansı, büyük-küçük tüm tanecikler için eşittir (Pakkenberg ve Gundersen, 1988). Bu ilişkiden yola çıkılarak, belli bir hacimde bulunan taneciklerin toplam sayısı (veya sayısal yoğunlukları) hesaplanabilir.
Disektör taneciği, disektör metodu ile yapılan sayım sırasında sayılabilen taneciklere verilen isimdir. Fiziksel disektörde, sayım için alınan kesit çiftlerinden birisi örnek kesit (reference section) ve diğeri gözlem kesiti (look-up section) olarak kullanılır. Bu kesitler incelenir ve örnek kesitte bulunup, gözlem kesitinde bulunmayan tanecikler, disektör taneciği olarak sayıma dahil edilir ve “Q-” simgesi ile gösterilirler. Bunlar, disektör yüksekliği içerisinde örneklenebilmiş olan tanecik uçlarıdır (Şekil 8).
 |
| Şekil 8. Fiziksel disektör uygulamasının şematik şekli. Fiziksel disektör, ardışık veya birbirlerinden belli bir aralıkla ayrılmış olan iki fiziksel kesitin, aynı partiküllerin izdüşümlerini içeren ortak alanları karşılaştırılarak uygulanır. Kesitlerin ayrı ayrı fotoğrafları, iki ayrı mikroskoba bağlı monitörler, iki ayrı projeksiyon mikroskobu veya görüntü kaydetme yeteneği olan bir bilgisayar yazılımı gibi araçlarla, kesitlerde aynı örnekleme alanına karşılık gelen bölgeler bulunarak, karşılaştırılır. Kesitlerden birisi örnek, diğeri gözlem kesiti olarak adlandırılarak, örnek kesitte bulunup, gözlem kesitinde bulunmayan partikül izdüşümleri, disektör partikülleri (Q-) olarak sayılır. |
Disektör sayımı sırasında, örnek ve gözlem kesitleri, rolleri değiştirilerek, yani, örnek kesit olarak kullanılan kesit gözlem; gözlem kesiti ise örnek kesit olarak değerlendirilip, çift yönlü bir sayım da yapılabilir. Bu da, ilave kesit alma işlemine ihtiyaç duyulmadan disektör sayısının arttırılmasını, dolayısıyla daha fazla örnek üzerinde çalışabilmeyi mümkün kılar (Şekil 9).
 |
| Şekil 9. Disektör örneklerinin sayısını artırmak üzere, kesitlerin rolleri değiştirilerek iki yönlü bir disektör sayımı da uygulanılabilir |
Tanecik sayımı yapmak için tanecik izdüşümlerinden yararlanılan durumlarda, kesitlerde ortaya çıkan tanecik izdüşümlerinin belli bir alanla sınırlandırılarak sayılmaları gerekmektedir. Bu durumda, izdüşümlerin hangi kurallara göre sınırlandırılması gerektiği konusu ortaya çıkar. Klasik olarak uygulanan eski metotlarda, kare veya dikdörtgen yapıdaki bir çerçeve izdüşümler üzerine yerleştirilerek, doğrudan bu çerçeve içine düşen tanecik izdüşümlerinin sayılması, oldukça yaygın olarak kullanıla gelmiş olan bir yöntemdir. Daha sonraları ise, bu tip bir sayımın tanecik sayısını fazla hesap etmeye neden olduğu ortaya çıkınca, bu kez de basit olarak ortadan, köşegenlerinden biri boyunca ikiye ayrılmış olan bir sayım çerçevesi kullanılmaya başlanmıştır. Bu çerçevedeki sayım kuralı ise, çerçeve kenarlarının bir yarısına isabet eden taneciklerin sayılıp, diğer yarıya isabet edenlerin sayılmaması şeklindedir. Fakat bu çerçevenin de gerçek tanecik değerini vermekten uzak olduğu daha sonra tarafsız sayım çerçevesinin ortaya çıkışı ile anlaşılmıştır. Sayım çerçevelerinden kaynaklanan bu tip sayım hatalarının sebebi, “kenar etkisi” denen bir etki ile açıklanmaktadır. Kısa olarak kenar etkisi, herhangi bir sayım çerçevesi kullanıldığında, çerçevenin içine düşen taneciklerin sayılmasında bir sorun olmadığı halde, çerçeve kenarlarıyla kesişen taneciklerin hangi kurallara göre değerlendirilmeleri gerektiği sorununa vurgu yapmaktadır. En son haline 1970’li yıllarda Gundersen tarafından getirilen tarafsız sayım çerçevesi, yapılan hesaplamalarla, kenar etkisini en güvenilir biçimde ortadan kaldıran özelliklere sahiptir (Gundersen, 1977)
 |
| Şekil 10. Bir ekran üzerine yerleştirilmiş bir tarafsız sayım çerçevesi görülüyor. Kesikli çizgiler serbest ya da dahil kenarları, devamlı çizgiler ise yasak kenarları göstermektedir. Yasak çizgilerin uzantılarının doğrultuları, sayımın doğruluğu için gerekli ve önemlidir. |
 |
| Şekil 11. Tarafsız sayım çerçevesinden önce yaygın olarak kullanılmakta olan iki sayım çerçevesi tipi. Bu tiplerin farklı çeşitlemeleri mevcut olmakla beraber, burada sadece sayımda kullandıkları temel mantığı karşılaştırmak amacıyla bu iki temel tip şematize edilmiştir. Birinci çerçevede (A) kullanılan mantık, çerçevenin her noktasına temas eden ve içine denk gelen partikülleri saymaktır. Sağdaki ikinci çerçeve ise (B), sanal bir köşegen çizgisi ile, iki yarıya bölünmüş ve bir taraftaki kenarlar sayılabilir, diğer taraf ise sayılamaz alan olarak belirlenmiştir. Bu ayrımın amacı, birinci çerçeve tipinin sebep olduğu fazla sayımı ortadan kaldırmaktır. Fakat her iki çerçeve de, tarafsız sayım çerçevesi ile karşılaştırıldığında fazla partikül sayımına sebep oldukları açıkça gözlenmektedir (Şekil 16) (Gundersen, 1977’den değiştirilerek çizilmiştir). |
 |
| Şekil 12. Şekil-11'de gösterilen iki eski tip sayım çerçevesi ile tarafsız sayım çerçevesinin, teorik bir sayımla karşılaştırılması. Dokuz adet sayım alanına ayrılmış bir alanda, her bir alan birbirinden bağımsız olarak örneklenerek, burada bulunan partikül izdüşümlerinin, her bir sayım çerçevesi tipi tarafından nasıl sayıldığı gösterilmektedir. Her alanda, hangi çerçevenin kaç tane izdüşüm saydığı, çerçevelerin küçük şematik şekillerinin yanındaki sayılarla belirtilmektedir. Sonuçta, tüm alanlarda yapılan sayımlar toplandığında, sadece tarafsız sayım çerçevesinin gerçek partikül izdüşümü sayısını verebildiği görülmektedir. Bu kadar kısıtlı bir örnek içinde bile bu denli farklı sonuçlar elde edilebildiği dikkate alınırsa, çok daha fazla sayıda partikül ve alanın örneklendiği biyolojik çalışmalarda bu hata payının daha büyük olabileceği rahatlıkla söylenebilir (Gundersen, 1977’den faydalanılarak çizilmiştir). |
 |
| Şekil 13. Bir başka tip tarafsız sayım çerçevesi ile döşenmiş bir alan gösterilmektedir. Tarafsızlık ve doğru örnekleme gereklerini yerine getiren her çerçeve, tarafsız sayım çerçevesi olarak kullanılabilir. Bu dairesel çerçeve durumunda da dahil kenarlar kesikli, yasak kenarlar kalın çizgiler ile belirtilmekte ve bu yasak kenarlar da görüntü alanı boyunca uzanmaktadırlar (Gundersen, 1977). |
Tarafsız sayım çerçevesi, en genel olarak kullanılan şekliyle, bir kalın ve düz, bir de ince ve kesikli iki tip çizgi ile sembolize edilen dört kenara sahip basit bir dikdörtgen veya karedir. Görünüşte pek fazla bir değişikliği olmamasına rağmen, sayım kuralları açısından diğer sayım çerçevelerinden farklıdır. Temel olarak, ince ve kesikli çizgiler “dahil” kenarlar, kalın ve devamlı çizgiler de “hariç”veya “yasak” kenarlardır. Yani kesikli çizgilere rastlayan izdüşümler sayılırken, devamlı çizgilere isabet eden izdüşümler sayım dışı bırakılır (Şekil 10-12). Tarafsız sayım çerçevesinin en önemli özelliği, yasak kenarların uzantılarıdır. Bu uzantılar, çerçevenin yerleştirildiği görüntü alanının tamamını kaplayacak şekilde uzatılırlar.
Tarafsız sayım çerçevesi, tanecik sayımı için, halihazırdaki en etkin ve güvenilir sayım çerçevesidir. Bu çerçevenin tanecik izdüşümlerini en doğru biçimde saymayı sağladığı, geometrik hesaplamalarla da kanıtlanmıştır (Gundersen, 1977).
Optik Disektör ve 3 Boyutta Tanecik Sayımı
Disektör sayım metodu, temel mantığı uyarınca oldukça basit ve etkin olmasının yanında, fiziksel disektör uygulaması kimi zorlukları da beraberinde getirmektedir. Bunlardan en önemlisi, iki ayrı kesitte çalışmak ve birbirini takip eden bu iki kesitte aynı olan alanları bularak, bunları ayrı ayrı görüntüler halinde (fotoğraf, projeksiyon mikroskobu veya monitör gibi araçlar yardımıyla) karşılaştırmanın zorunlu olmasıdır. Aslında, stereolojik metotların uygulama alanına girmesinden önce uygulanan metotlar, ya oldukça yetersiz bir doğruluğa sahip veya yüksek bir doğruluk ihtimali içermekle birlikte çok uzun zaman ve emek alan bir çalışma dizaynı gerektiren yöntemlerden oluşmaktaydı. Disektör prensibi, doğruluk ve az zamanda daha az değişkenlik (varyasyon) gösteren verilerin elde edilebilmesi gibi iki önemli kriteri bir araya getirmektedir. Fakat yine de, özellikle bazı çalışmalarda (örneğin insan neokorteksindeki toplam nöron sayısının hesaplanması gibi karmaşık bir çalışmada), fiziksel disektör uygulaması uzun zaman alabilecek bir takım işlemler gerektirmektedir. Elektron mikroskobu ve bazı özel (kalın kesitlerin kullanılamadığı) durumlarda ışık mikroskobu düzeyindeki çalışmalarda kullanılması zorunlu olan fiziksel disektör, ışık mikroskobunda tanecik sayımı için tek alternatif değildir. Işık mikroskobu düzeyindeki birçok çalışmada kullanılabilecek nispeten daha yeni bir yöntem, prensipleri 1986 yılında Gundersen tarafından tarif edilen optik disektör veya “sayım kutusu”dur (counting box; Williams and Rakic, 1988).
Optik disektör sayım metodunun esası, kalın bir doku kesiti içerisinde, sanal optik kesitlerle ilerleyerek tanecik sayımı yapmaktır (Şekil 14 ve 15). Bu sayım yönteminin tek şartı, sayılması düşünülen taneciklerin kesit alma doğrultusuna dik olan yüksekliklerinden daha fazla kalınlığa sahip kesitler elde etmektir. Her doku için gereken kesit kalınlığı farklı olmakla beraber, sinir dokusunda yapılacak bir nöron sayım çalışması için, boyama ve kapatma işlemlerinden sonra ortalama 20-25 mikrometre kalınlığa sahip olan kesitlerin alınması yeterlidir.
 |
| Şekil 14. Optik disektör sondasının üç boyutlu şematik çizimi. Optik disektör, fiziksel olarak karşılaştırılan iki kesit çifti yerine, kalın bir kesit hacmi içerisinde, bir dizi sanal optik kesitle ilerleyerek, karşılaşılan partikülleri sayma esasına dayanır. Teorik olarak, kalınlık içindeki her sanal kesit, bir sonrakine göre örnek (referans) kesit, bundan bir sonraki kesit ise öncekine göre gözlem (look-up) kesitidir. Dolayısıyla birinde bulunup diğerinde bulunmayan partiküller, disektör partikülü olarak sayılırlar. Fakat pratik uygulamada, sayısal açıklığı yüksek bir mercek (Daha ince optik kesitler alabilmek için gereklidir.) kullanılarak, kesit kalınlığı ve disektör sondasının yüksekliği boyunca tarama yapılarak, karşılaşılan partiküller sayılır (Çeşitli kaynaklardan yararlanılarak çizilmiştir). |
 |
| Şekil 15. Sayım alanının bir kesit içinde ilerletilmesi ile oluşturulan sanal bir sayım kutusu (optik disektör sondası). Bu hacimde bulunan partiküller, önceden yapılan kabullere uygun olarak sayılırlar. Sayım kutusunun, üst sınırları siyah kalın çizgiler ile belirlenmiş yüzeylerine temas eden partiküller sayım dışı bırakılırken, diğer kenarlara değen ve kutunun tamamen içinde kalan partiküller sayılır. En üst ve en altta bulunan yüzeyler ise optik disektör sondasının veya sayım kutusunun üst ve alt sınırları olup, bunlardan birine temas eden partiküller sayılırken, diğerine temas edenler sayım dışı bırakılır. Buradaki karar, bir hayvandaki tüm örnekleme alanları boyunca aynı şekilde uygulanmak şartı ile, araştırıcının kendisine kalmaktadır. Şekilde, (+) işaretli partiküller sayılabilirken, (-) işaretli olanlar sayım dışı bırakılmaktadırlar (Burada üst yüz “hariç”, alt yüz ise “dahil” olarak kabul edilmektedir) (Çeşitli kaynaklardan yararlanılarak çizilmiştir). |
 |
| Şekil 16. Civciv beyin kesitleri üzerinde uygulanan optik parçalama yönteminin şematik açıklaması. Optik parçalama yöntemi, belli adım aralıklarıyla (x ve y) doku kesiti üzerinde ilerleyerek, her adımda belli bir alanın, üç boyutlu optik sondalarla taranması ile gerçekleştirilir. Üstte, bu adımların yerleşimi gösterilmektedir (Sarı renkli alan hippokampusu temsil etmektedir.). Bu adımlardan, sadece ilgilenilen alan (hippokampus) üzerine isabet edenlerde sayım yapılır. Optik sonda (veya üç boyutlu sayım kutusu; optik disektör sondası) ise, doku kalınlığı içerisinde belli bir kalınlığın, optik olarak taranması ile elde edilir (alt kısımda bu adımlardan birinin ve içindeki optik disektör sondasının büyütülmüş şekli görülmekte). Görüntü üzerine yerleştirilen bir sayım çerçevesi (A), kesit görüntüsü içerisinde optik olarak ilerletildikçe, doku içerisinde sanal bir sayım kutusu oluşturur. Bu kutunun, sayım çerçevesinin yasak kenarları tarafından oluşturulan yüzeylerine değen partiküller sayım dışı bırakılırken, diğer kenarları tarafından oluşturulan yüzeylere değen veya tamamen içinde kalan partiküller sayıma dahil edilir. Disektör sondasını oluşturan sayım çerçevesinin veya sayım alanının, x ve y adımlarından oluşan adım alanlarına bölünmesi ile, o sonda tarafından örneklenen alan oranı bulunur. Optik disektör sondası, kesit yüzeyi artefaktlarından korunmak amacıyla, kesitin alt ve üst yüzeylerinden belli bir mesafe uzakta olacak şekilde ayarlanmalıdır. Bu mesafelere alt (G1) ve üst (G2) güvenlik kuşakları denir. Disektör sondasının yüksekliği (h), sayım çerçevesinin alanı (A) ile çarpıldığında, disektör hacmi elde edilir. Disektör sondası ile örneklenen kalınlık parçası ise, disektör sondası yüksekliğinin (h), kesit kalınlığına (t) bölünmesi ile elde edilir. Pratikte de kesit kalınlığı olarak ortalama kesit kalınlığı değeri kullanılır (bkz. metin). |
Kesit Kalınlığının Ölçülmesi
Kesit kalınlığı, tanecik sayısı hesaplamalarında önemlidir. Fiziksel parçalama dışındaki metotlarda, tanecik sayısına ulaşmak için, sayım yapılan hacim değerinin bilinmesi gerekmektedir. Hacim değeri ise, sayım alanı ve sayım “kalınlığı”nın bilinmesini gerektirir.
Kesit kalınlığı, ışık mikroskobu düzeyinde olduğu kadar, elektron mikroskobu çalışmalarında da önemlidir. Kesit kalınlığını ölçmek için bir çok metot kullanılıyor olsa da, burada sadece, çalışmada kullanılan metot üzerinde durulacaktır.
Stereolojik metotların uygulanmasında, kesit kalınlığını (ışık mikroskobunda) ölçmek için genellikle, odaklama değişimi sırasında mikroskop tablasının dikey eksende (z ekseninde) kat ettiği mesafe hesaplanır. Bu mesafe değişimi de genellikle, ya mikroskobun mikro veya makro vidasının üzerinde bulunan derecelendirmeler kullanılarak veya, mikroskop tablasına takılan ve tablanın dikey eksendeki hareketlerine duyarlı bir araç (mikrokator) yardımıyla gerçekleştirilir. Fakat mikroskobun vidalarının üzerinde bulunan derecelendirme, genelde vidaların zıt dönüş yönleri arasında bulunan boşluklardan (backlash) dolayı hassas değildir ve her zaman güvenilir biçimde kullanılamazlar. Fakat, bu vidalar üzerinde bulunan skalalar genişletilerek, daha güvenli bir ölçüm yapılması sağlanabilir (Korkmaz ve Tümkaya, 1997).
Elektronik veya mekanik mikrokatorlar ise, çok daha hassas ölçüm yapan araçlardır. Eskiden kullanılan mekanik tipleri halen bulunduğu gibi, şu anda daha yaygın olarak elektronik donanımlı olanlar kullanılmaktadır. Elektronik mikrokator, bir dijital gösterge ve bir hareket algılayıcısından oluşur. Hareket algılayıcısının mikroskop tablasında tespit ettiği dikey konum değişiklikleri, mikrokatorun dijital göstergesinden mikrometre (m m) seviyesinde okunur. Genellikle, dijital mikrokatorlar, 0.1m m hassaslıktadırlar.
Mikrokator veya benzer bir araç ile kesit kalınlığı veya kesit içerisinde bir kalınlık tespit edilirken, kesitin alt ve üst yüzeyleri, değişik seviyelerdeki odaklamalarla, araştırıcı tarafından belirlenmelidir. Mikroskop görüntüsü, kesitin üst yüzeyine yaklaştırıldığında, ilk net görüntünün elde edildiği yer kesitin üst yüzü; son karşılaşılan net görüntü ise, kesitin alt yüzüdür. Bu ikisi arasında optik olarak ilerlerken mikroskop tablasına yaptırılan aşağı veya yukarı hareketler, kesit kalınlığını verecektir.
Bu yöntemle kesit kalınlığı hesaplanırken, araştırıcılar arasında, kesitin üst ve alt yüzeylerini belirlemede kullandıkları kabullerin farklılığından dolayı, değişik sonuçların ortaya çıkması mümkündür. Fakat bu fark, özellikle kullanılan kesitler 30m m’den büyükse ve plastik gömme ortamı kullanılmışsa, tüm çalışma içinde önemsenmeyecek kadar küçük bir hata payına sebep olur.
Parçalama (the fractionator)
Stereolojide parçalama yöntemi, şu anda belki de stereolojinin en çok kullanılan tanecik sayma (veya alan, hacim, uzunluk vb. hesaplama) yöntemidir. Dokuda meydana gelen hiçbir şekil değişiminden etkilenmemesi, kesit kalınlığı, büzüşme-şişme miktarı gibi değerlere ihtiyaç göstermemesi ve oldukça etkin bir yöntem olması açısından, en çok tercih edilen metotların başında gelir.
Parçalama yönteminin esası, herhangi bir yapıdan, tek tip (uniform) sistematik rasgele örnekleme ile seçilen nispeten küçük bir doku parçasında tanecik sayımı yapmaktır. Gereken tek şart, sayım için örneklenen doku miktarının, orijinal yapının kaçta kaçına karşılık geldiğinin, yani ana yapıya olan oranının bilinmesidir. Bu küçük doku bölümünden elde edilen tanecik sayısı değeri ise, sadece bu küçük parçanın, ana yapıya olan oranı ile çarpılarak, toplam sayının elde edilmesinde kullanılır. Söz konusu olan sadece örnekleme (parçalama) oranı olduğundan, kesit kalınlığı, deformasyon derecesi ve doku hakkında herhangi bir ön kabul yapmaya gerek kalmamaktadır. Parçalama yöntemi o kadar kolay, tarafsız ve etkin bir yöntemdir ki, taraflı bir parçalamanın (fraksiyonlama) nasıl yapılacağı bilinmemektedir! (Gundersen ve ark., 1988a, 1988b).
Parçalama yöntemi aslında, bir tanecik sayım yöntemi olmaktan çok, bir örnekleme planıdır. Parçalama yöntemi ile örneklenen dokuda disektör sayım metodu kuralları uyarınca sayım yapmayı içeren bu bileşke yöntem, tanecik sayımında kullanılan disektör uygulamasının tipine göre, optik ve fiziksel olarak ikiye ayrılmaktadır. Temel mantık her iki yöntemde de aynı olmakla beraber, uygulamada bazı farklılıklar mevcuttur.
Fiziksel Parçalama (the physical fractionator)
Fiziksel parçalama, parçalama örneklemesi ile fiziksel disektör sayım metodunun bir bileşkesidir. Temelde aynı mekanizma ile uygulanmasına rağmen, optik parçalama ile bir takım uygulama farklılıkları vardır. Tatbik etme şekli açısından, bazı durumlarda kullanılamaz, fakat optik parçalama yöntemi için de aynı durum söz konusudur.
Fiziksel parçalama, tanecikleri sayılacak olan yapının, belli adımlarla daha küçük fiziksel parçalara ayrılarak örneklenmesi ve en son örnekleme neticesinde elde kalan oranı belli parçalardan, toplam tanecik sayısını elde etmek şeklinde özetlenebilir. Parçalama yönteminin temelinde, sistematik rasgele örnekleme mantığı yatmaktadır. Çalışılan yapıdan çeşitli aşamalarda alınan örneklemelerde uyulması gereken tek şart, sistematik ve rasgele olarak örnek seçimidir; yani ilk m tane örneği içeren aralık içinden rasgele bir başlangıç örneği seçilerek, daha sonra bu seçilen örneği takip eden her m’inci örnek alınmalıdır. Burada m, önceden karar verilen örnekleme aralığıdır (sözgelimi, her 20 kesitten birinin seçilmesine karar verilmişse m, 20 dir).
Parçalama metodunun bir diğer özelliği de basamaklı örneklemedir. Her basamakta, ihtiyaç duyuldukça, eldeki örneklerden, bilinen bir oranda sistematik ve rasgele olarak örnekleme yapılır. Bir sonraki basamakta ise, önceki örnekleme basamağında seçilen örnekler arasından yeni bir örnekleme yapılır. Her bir örneklemede, örnek olarak seçilen parça veya kesitlerin, örneğin alındığı yapı veya örneklerin ne kadarlık bir oranına karşılık geldiği bilinmelidir. Bu değer, parçalama katsayısı olarak adlandırılır ve “f” ile gösterilir (West ve ark., 1996).
Parçalama metodunda esas amaç, tüm stereolojik metotlarda olduğu gibi, çalışılan yapının belli bir oranına karşılık gelen ve mümkün olduğunca küçük olan bir parçası üzerinde, belli ve kabul edilebilir bir hata payı dahilinde sonuçlar elde etmektir. Yöntem, doğası itibariyle tarafsız olduğundan, örnekleme sayısı arttırıldıkça gerçek değere daha çok yaklaşan sonuçlar elde etmek mümkün olacaktır. Dolayısıyla, önceden belirlenen (genellikle %10’dan küçük) bir hata payı içerisinde sonuçlar elde edebilmek için de, ön çalışma sırasında, hata katsayısına en fazla etkisi olan değişken belirlenmelidir. En az 5 hayvan üzerinde yapılacak bir ön çalışma, hata oranının ve buna katkısı olan etkenlerin belirlenmesi için yeterlidir. Tek bir hayvanda yapılan bir ön çalışma, çalışma planının uygunluğu hakkında bir fikir veremez, çünkü, genel bir kural olarak, sonuçların değişkenliğine en büyük katkı her zaman, bireyler arasında bulunan farklılıklardan (biyolojik farklılıktan (varyasyondan)) gelmektedir. Bunu hesaba katmak için ise, ilk yapılacak şey, bireyler arasındaki farklılıkları ortaya koyabilecek bir ön çalışma ile işe başlamaktır. İstenen hata katsayısının sağlanması durumunda, her aşamada rahatlıkla örnekleme yapılabilir (Gundersen ve Jensen, 1987).
Fiziksel parçalama yönteminde, çalışılan yapı bir dizi parçalama dizisine tabi tutulur. Her bir aşamada sistematik ve rasgele olarak seçilen parçaların oranları kaydedildikten sonra, elde kalan son örnekler bloklara gömülerek sonuna kadar kesitlere ayrılır. Bu kesitlerden de istenen oranda sistematik ve rasgele örnekler alınır. Daha sonra, mikroskop altında hücre sayımı yapılırken de, sayım alanları arasından örnekleme yapılabilir (Şekil-4). Tek şart, sistematik ve rasgele yapılan bu örnek seçimlerinin “parçalama oranlarını” bilmektir. Tüm örneklemeler yapıldıktan sonra gerçekleştirilen tanecik sayımı sonucunda elde edilen tanecik sayısı değeri, çalışılan yapının o kadar bölümünde kaç tanecik bulunduğunu belirtir. Bu sayı, örnekleme oranlarının tersleri ile çarpılarak, toplam tanecik sayısı hesaplanır. Bu işlem kısaca şu şekilde formüle edilebilir:
Temel mantığından da anlaşılacağı gibi, yöntem tamamıyla tarafsızdır. Çalışılan yapı ile ilgili hiçbir ön kabul yapılması gerekmediği gibi, parçalama oranlarından başka (kesit kalınlığı, deformasyon sabiti vb) bir veriye de ihtiyaç göstermemektedir. Doğru bir biçimde uygulandığında, örnekleme sayısı ne kadar arttırılırsa, gerçek değere o kadar yaklaşan bir hesaplama sağlar. Taneciklerin parçalama yöntemi ile örneklenmesi, onların sadece fiziksel varlığına bağlıdır. Yani varsa örneklenir, yoksa örneklenemezler. Var olan taneciklerin tümü de eşit oranda örneklenme şansına sahiptirler. Ayrıca, çok az miktarda örnek üzerinde çalışarak, oldukça kısa zamanda, istenen değişkenlik sınırları içerisinde sonuçlar almayı da sağladığından en etkin yöntemlerden bir tanesidir (West ve ark., 1991).
Optik Parçalama (the optical fractionator)
Optik disektörün uygulanmaya başlamasından sonra, optik parçalama yöntemi de kendiliğinden ortaya çıkmıştır. Optik parçalama kısaca, basamaklı örneklemelerden elde edilen ve tüm yapıya olan oranı (parçalama oranı) bilinen örnekler üzerinde, optik disektörler ile tanecikleri örneklemektir. Uygulanması, fiziksel parçalamaya göre çok daha kolaydır ve daha az zaman alan bir metottur. Bu kolaylık, optik disektör uygulamasının sağladığı kolaylıklardan kaynaklanmaktadır. İki ayrı fiziksel kesitin karşılaştırılması zorunluluğu bulunmadığından, çok daha yaygın olarak kullanılan bir metottur. Özellikle sinir sistemi ile ilgili çalışmalarda yaygın olarak kullanılan optik parçalama, bazı durumlarda, fiziksel parçalamada olduğu gibi uygulanamamaktadır. Kalın kesitlerin alınamaması, kesitlere boya nüfuzunda zorluk, büyük yapıların söz konusu olduğu çalışmalar gibi durumlarda, fiziksel parçalama kullanılması bir zorunluluktur.
Optik parçalama yöntemi, uygulama kolaylığı sebebiyle, en çok tercih edilen tanecik örnekleme yöntemidir. Sadece tanecik sayımında değil, tanecik çapı, yüzey alanı ve hacim hesaplamaları gibi uygulamalarda da sıklıkla kullanılmaktadır. Yöntemin uygulanmaya başlanmasından bu yana, oldukça ilginç sonuçlar elde edilmiştir. Sözgelimi, insan beyin hücrelerinin toplam sayısının hesaplanmasında en büyük problemlerden birini oluşturan beyincik granüler hücrelerinin sayısı, optik disektör ve Cavalieri kombinasyonunun kullanılması ile ortaya konmuştur (Andersen, 1992). Ayrıca, uzun yıllardan beri, yaşlanmaya bağlı olarak meydana gelen hafıza kaybı (demans) olaylarının açıklanmasında kullanılan hippokampus ve ilişkili yapılarda meydana gelen yaşa bağlı nöron kaybı olduğu konusunda, yaşlı ve hafıza bozukluğu gösteren sıçanlarda optik parçalama yöntemi ile yapılan çalışmalar sonucunda aksi yönde kanıtlar elde edilmiştir (Gallagher ve ark. 1996; Rasmussen ve ark. 1997, Şekil 16).
KAYNAKLAR
1. Abercrombie, M., (1946), Estimation of nuclear populations from microtome sections. Anatomical Record, 94, 239-247.2. Andersen, B.B., Korbo, L., Pakkenberg, B.(1992) A quantitative study of the human cerebellum with unbiased stereological techniques. J. Comparative Neurology, 326:549-560.
3. Braendgaard, H., Evans, S.M., Howard, C.V., Gundersen, H.J.G., (1990). The total number of neurons in the human neocortex unbiasedly estimated using optical disectors. J. Microscopy, 157: 285-304
4. Clarke, P.G.H., (1992). How inaccurate is the Abercrombie correction factor for cell counts?. TINS, 15(6): 211-212
5. Cruz-Orive, L.M.(1997) Stereology of single objects. J. Microscopy, 186(2), 93-107
6. Cruz-Orive, L.M., Weibel, E.R.(1990) Recent stereological methods for cell biology: a brief survey. Lung. Cell. Mol. Physiol., 2, L148-L156
7. Gallagher, M., Landfield, P.W., McEwen, B., Meaney, M.J., Rapp, P.R., Sapolsky, R., West, M.J. (1996). Hippocampal neurodegeneration in ageing. Science, 274, 4-5.
8. Gundersen, H.J.G (1986) Stereology of arbitrary particles. J. Microscopy, 143(1), 3-45
9. Gundersen, H.J.G. (1977) Notes on the estimation of the numerical density of arbitrary particles: The edge effect. J. Microscopy, 111: 219-223
10. Gundersen, H.J.G. (1992). Stereology: The fast lane between neuroanatomy and brain function or still only a tightrope? Acta Neurologica Scandinavica, 137, 8-13.
11. Gundersen, H.J.G., Bagger, P., Bendtsen, T.F., Evans, S.M., Korbo, L., Marcussen, N., Moller, A., Nielsen, K., Nyengaard, J.R., Pakkenberg, B., Sorensen, F.B., Vesterby, A., West, M.J. (1988a). The new stereological tools: Disector, Fractionator, nucleator, and point sampled intercepts and their use in pathological research and diagnosis. APMIS, 96, 857-881.
12. Gundersen, H.J.G., Bendtsen, T.F., Korbo, L., Marcussen, N., Moller, A., Nielsen, K., Nyengaard, J.R., Pakkenberg, B., Sorensen, F.B., Vesterby, A., West, M.J. (1988b). Some new, simple, and efficient stereological methods and their use in pathological research and diagnosis. APMIS, 96, 379-394.
13. Gundersen, H.J.G., Jensen, E.B. (1987). The efficiency of systematic sampling in stereology and its prediction. J. Microscopy, 147(3):229-263.
14. Howard, C.V., Reed, M.G. (1998) Unbiased Stereology: Three dimensional measurement in microscopy, Bios Scientific Publishers, U.K.
15. Korbo, L., Pakkenberg, B., Ladefoged, O., Gundersen, H.J.G., Arien-Soborg, P., Pakkenberg, H.(1990) An efficient method for estimating the total number of neurons in rat brain cortex. J. Neuroscience Methods, 31, 93-100
16. Korkmaz, A. Tümkaya, L., (1997) Estimation of section thickness and optical disector height with a simple calibration method. J. Microscopy,187(2): 104-109
17. Mayhew, T.M., (1991). Review article: The new stereological methods for interpreting functional morphology from slices of cells and organs. Experimental Psysiology, 76: 639-665
18. Mayhew, T.M., (1992).A Review of recent advances in stereology for quantifying neural structure. J. Neurocytology, 21, 313-328
19. Mayhew, T.M., (1996) Invited Review: Adaptive remodelling of intestinal epithelium assessed using stereology: correlation of single cell and whole organ data with nutrient transport. Histol Histopathol, 11, 729-741
20. Mayhew, T.M., Gundersen, H.J.G. (1996). If you assume, you can make an ass out of u and me: A decade of the disector for stereological counting of particles in 3D space. J. Anatomy, 188:1-15.
21. Oorschot, D.E. (1994). Are you using neuronal densities, synaptic densities or neurochemical densities as your definitive data? There is a better way to go. Progress in Neurobiology, 44, 233-274.
22. Pakkenberg, B., Gundersen, H.J.G. (1988) Total number of neurons and glial cells in human brain nuclei estimated by the disector and the fractionator. J. Microscopy 150(1):1-20.
23. Pakkenberg, B., Gundersen, H.J.G. (1997). Neocortical neuron number in humans: Effect of sex and age. J. Comparative Neurology, 384, 312-320
24. Pakkenberg, H., Andersen, B.B., Burns, R.S., Pakkenberg, B.(1995). A stereological study of substantia nigra in young and old rhesus monkeys. Brain Research, 693, 201-206
25. Rasmussen, T., Schliemann, T., Sorensen, J.C., Zimmer, J., West, M.J. (1996). Memory impaired aged rats: No loss of principal hippocampal and subicular neurons. Neurobiology of Ageing, 17(1), 143-147.
26. Sterio, D.C.(1984). The unbiased estimation of number and sizes of arbitrary particles using the disector. J. Microscopy, 134(2), 127-136
27. West, M.J. (1993). New stereological methods for counting neurons. Neurobiology of Ageing, 14, 275-285.
28. West, M.J. (1994).Advances in the study of age-related neuron loss. Seminars in Neuroscience, 6, 403-411
29. West, M.J., Æstergaard, K., Andreassen, O.A., Finsen, B., (1996). Estimation of the number of somatostatin neurons in the striatum: An in situ hybrizidation study using the optical fractionator method. J. Comparative Neurology 370, 11-22
30. West, M.J., Gundersen, H.J.G., (1990). Unbiased stereological estimation of the number of neurons in the human hippocampus. J. Compararative Neurology, 296, 1-22.
31. West, M.J., Slomianka, L.,Gundersen, H.J.G. (1991). Unbiased stereological estimation of the total number of neurons in the subdivisions of the rat hippocampus using the optical fractionator. The Anatomical Record, 231, 482-497.
32. Willams, W. R., Rakic, P., (1988). Three-Dimensional counting: An accurate and direct method to estimate numbers of the cells in sectioned material. J. Comparative Neurology 278, 344-352
Bu bölümdeki bilgi ve şekiller, Samsun Ondokuz Mayıs Üniversitesi Tıp Fakültesi Fizyoloji Anabilim Dalı Araştırma Görevlisi ve Stereoloji Derneği kurucu üyelerinden olan Sinan CANAN'ın, Sağlık Bilimleri Enstitüsü Histoloji-Embriyoloji Anabilim Dalında Doç. Dr. Süleyman KAPLAN'ın danışmanlığında tamamladığı "Geçici Serebral İskemi Sonrası Civciv (Gallus domesticus) Hippokampusunda Meydana Gelen Nöron Sayısı Değişikliklerinin Optik Fraksiyonlama Yöntemi İle Araştırılması" başlıklı yüksek lisans tezinden değiştirilerek alınmıştır. Buradaki tüm bilgi ve görsellerin yayın hakkı Türk Stereoloji Derneği'ne aittir.
